En general, la operación módulo es una operación aritmética usada para obtener
el residuo en una división.
Usualmente, el valor de interés en una división es el cociente, sin embargo,
obtener el residuo puede ser útil para sacar conclusiones sobre el dividendo
y el divisor de la operación.
Lo típico al usar la operación módulo es que sus operandos sean números enteros
positivos, pero no está limitada a ellos, pues se puede aplicar también sobre
números negativos, y racionales de punto flotante (float) y de doble precisión
(double).
El operador %
En C++ se utiliza el operator% el cual es un operador aritmético, binario,
multiplicativo, sobrecargable, y de alta precedencia1. Tiene la misma
precedencia que la multiplicación y la división.
Pero tantos adjetivos calificativos pueden llegar a confundir. Al final del
día ¿Para qué sirve la operación módulo? El resultado de la operación puede
indicar si el divisor es múltiplo del dividendo, es decir, que el dividendo es
divisible por el divisor. Si dividendo % divisor == 0.
En código
Para determinar los números de una colección que son o no son múltiplos de 5:
#include <cmath> // Contiene el operator%
#include <print> // Para std::println desde -std=c++26
#include <vector>
int main() {
std::int32_t n = 5;
std::vector numeros{2, 4, 6, 8, 10, 15, 20, 42};
auto esMultiplo =
[](std::int32_t a, std::int32_t n)
{
return (a % n == 0);
};
for (const auto &numero : numeros)
std::println("{} es múltiplo de {}?: {:<}",
numero,
n,
esMultiplo(numero, n));
}
El resultado imprime
2 es múltiplo de 5?: false
4 es múltiplo de 5?: false
6 es múltiplo de 5?: false
8 es múltiplo de 5?: false
10 es múltiplo de 5?: true
15 es múltiplo de 5?: true
20 es múltiplo de 5?: true
42 es múltiplo de 5?: false
Para imprimir solamente los números que sí son múltiplos de 5:
#include <algorithm>
#include <cmath>
#include <print>
#include <vector>
//...
std::int32_t n = 5;
std::vector numeros{2, 4, 6, 8, 10, 15, 20, 22};
std::print("Múltiplos de {}: ", n);
auto imprimeMultiplosDeN =
[=](int a)
{
if(a % n == 0)
std::print("{} ", a);
};
std::ranges::for_each(numeros, imprimeMultiplosDeN);
//..
El resultado imprime
Múltiplos de 5: 10 15 20
Es bisiesto
Pero de nuevo, ¿Para qué nos sirve conocer si un número es divisible por 5? Bueno, una aplicación sencilla del uso del módulo es para conocer si el año ingresado a una función es bisiesto o no. Lo es cuando el año es divisible por 4, pero no es divisible por 100, a menos que sí sea divisible por 400:
#include <cmath>
#include <print>
bool esBisiesto(const std::int32_t& year)
{
return ( ((year % 4 == 0) && (year % 100 != 0))
|| (year % 400 == 0) );
}
int main()
{
const std::int32_t year = 2024;
const bool result = esBisiesto(year);
std::println("El año {} es bisiesto?: {}", year, result);
}
El año 2024 es bisiesto?: true
Otro ejemplo
El escenario es el siguiente: se quiere dibujar en la pantalla una matriz de
celdas (tiles) de tamaño columnas * filas. Las celdas están distribuidas en
filas y columnas, y se almacenan en un arreglo bidimensional. Al presionar sobre
una de las celdas ella cambia de color.
matriz<columnas, filas> celdas; // matriz[x][y]
Suponiendo que las celdas tienen un tamaño de 64 píxeles cada una, un punto en
la pantalla no corresponde necesariamente a una fila y una columna sino un lugar
dentro de una celda. Al dar clic dentro de una de las celdas la posición será un
punto (x,y) con las coordenadas.
Para identificar el índice columna-fila en el que se encuentra la celda dentro de la matriz se puede utilizar la operación módulo de la siguiente manera:
//...
Point point{179, 167};//La posición en pantalla al hacer clic
const std::size_t tile_size = 64;
const auto& [x, y] = point;
const std::size_t col = (x - (x % tile_size)) / tile_size;
const std::size_t row = (y - (y % tile_size)) / tile_size;
std::println("Punto : ({},{}) px ", x, y);
std::println("Posición: ({},{}) ", col, row);
//...
Resultando en
Punto : (179,167) px
Posición: (2,2)
Lo cual se puede visualizar así:
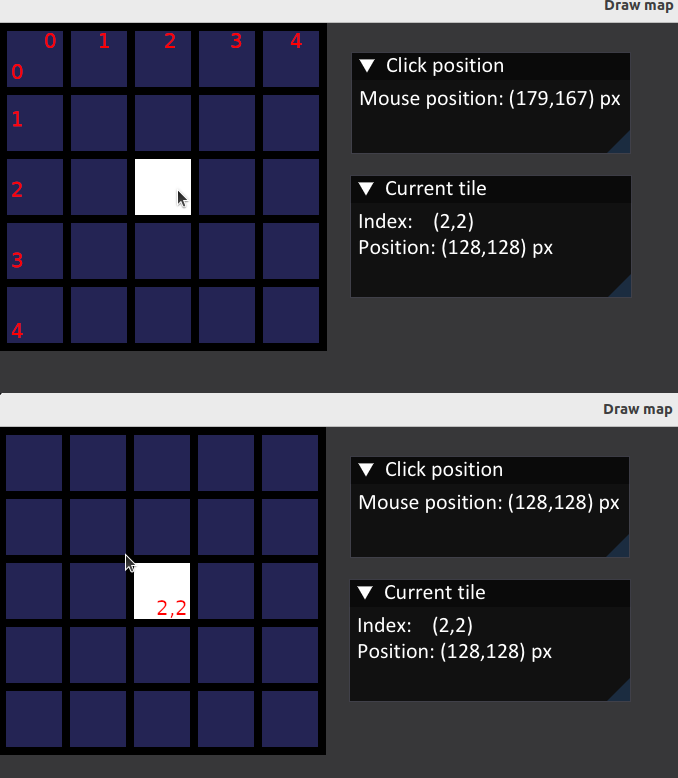
El racionamiento detrás de esto es que el módulo entre la posición y el tamaño de la celda es la diferencia entre el punto de origen de la celda y el punto de clic dentro de esa celda.
columna = (x - (x % tamaño_celda)) / tamaño_celda;
diferencia : 179 % 4 = 51
posicion_normalizada: 179 - 51 = 128
columna : 128 / 64 = 2
Al normalizar la posición con relación a las celdas (128, 128) basta con
dividirla entre el tamaño de la celda para encontrar el índice de la columna y
fila a la que corresponde (2, 2), con las siguientes consideraciones:
- El tamaño de la ventana está en píxeles
- El origen de la pantalla (0,0) está en la esquina superior izquierda
- El origen de cada celda también está en su esquina superior izquierda
- La primera celda comienza en el índice (0,0): columna cero, fila cero.
- Las colecciones en C++ comienzan en el índice cero.
Enteros negativos
En la biblioteca estándar existe la función
matemática para la división std::div
la cual realiza el cómputo del cociente y el residuo. Esta función permite
encontrar el módulo para números negativos.
//...
const auto result = std::div(7, -2);
std::println("cociente {}, residuo {}", result.quot, result.rem);
// cociente -3, residuo 1
Pues (-2 * -3) + 1 = 7
Signal 8: SIGFPE
La operación módulo es similar a la división en cuanto a que si se intenta dividir por cero el programa emitirá una señal, SIGFPE: Signal floating-point exception2. Igual sucede si se intenta calcular el módulo sobre cero.
//...
int m = 2 / 0;
//...
warning: division by zero [-Wdiv-by-zero]
7 | int m = 2 / 0;
| ~~^~~
Program returned: 136
Program stderr
Program terminated with signal: SIGFPE
Números racionales
Al intentar usar el operador sobre números de punto-flotante se genera un error:
float a = 4.0F;
float b = 2.0F;
float remainder = a % b;
// error: invalid operands of types 'float' and 'float'
// to binary 'operator%'
Para poder trabajar con números de punto flotante existen las funciones
std::remainder
y std::fmod.
Estas dos funciones difieren en la precisión con la que se calcula el cociente
para hallar el residuo. La ecuación para calcular el módulo es la siguiente:
rem = x % y
rem = x - quo * y
Donde
quo = x / y
Siendo quo = quotient = cociente
El std::remainder redondea el cociente al entero más cercano, mientras que el
std::fmod lo trunca.
float a = 5.1;
float b = 3.0;
float rem = std::remainder(a, b);
float fmod = std::fmod(a, b);
std::println("{:<10} of {} % {} = {}", "remainder", a, b, rem);
std::println("{:<10} of {} % {} = {}", "fmod", a, b, fmod);
Resultando en:
remainder of 5.1 % 3.0 = -0.9000001
fmod of 5.1 % 3.0 = 2.1
Siendo quo = 5.1 / 3.0 = 1.6999999
Entonces rem = x - quo * y
rem = 5.1 - (1.6999999 * 3.0) // redondea 1.69 a 2.0
rem = 5.1 - (2.0 * 3.0)
rem = 5.1 - 6.0
rem = -0.90
fmod = 5.1 - (1.6999999 * 3.0) // trunca 1.69 a 1.0
fmod = 5.1 - (1.0 * 3.0)
fmod = 5.1 - 3.0
fmod = 2.1



Deja un comentario