Pruebas de referencia: benchmark

Qué es benchmarking

En general, se refiere a realizar comparaciones de productos, servicios, o procesos para identificar cuáles funcionan de mejor manera, tienen mejor desempeño, u ofrecen ventajas sobre otros similares.

En programación se suelen usar las benchmarks, o pruebas de referencia, como una técnica para medir el rendimiento de un sistema o de uno de sus componentes.

Algunas bibliotecas de benchmark reconocidas son:

• Google Benchmark
• Hayai
• Celero
• Nonius

Catch2 y Nonius

En la versión 2.13.6 de la biblioteca de pruebas Catch2 se incluye a nonius como biblioteca para pruebas de referencia (micro-benchmarking).

Conan

El archivo conanfile para incluir a Catch2 en un proyecto CMake usando Conan contiene:

# conanfile.txt
[requires]
  catch2/2.13.6

[generators]
  cmake_find_package

Dado que Catch2 es solo-cabecera, basta con agregarlo al include_directories del objetivo a construir:

#...
set(CMAKE_MODULE_PATH ${CMAKE_MODULE_PATH} ${CMAKE_BINARY_DIR})
find_package(Catch2 REQUIRED)

target_include_directories(${PROJECT_NAME} 
        PRIVATE ${Catch2_INCLUDE_DIRS} )
#...

Micro-benchmarking en Catch2

Para usar las pruebas de referencia en Catch2 es necesario definir el macro que las activa antes de incluir el archivo de cabecera:

#define CATCH_CONFIG_ENABLE_BENCHMARKING
#include <catch2/catch.hpp>
//...

Es posible indicarle a Catch2 que use su main() en lugar de especificarle uno; esto se logra definiendo el macro CATCH_CONFIG_MAIN antes de incluir el archivo de cabecera, pero no es obligatorio.

Posteriormente, se crea un caso de prueba y dentro de este se crea la prueba de referencia, la cual se expande a una expresión lambda. Se incluye un return para evitar que el compilador optimice el código, y así la prueba sea más precisa.

Fibonacci

Un ejemplo de prueba de referencia es medir el tiempo medio de ejecución de un algoritmo implementado de diferentes maneras para conocer cuál puede ser más eficiente. En este caso se usa la Secuencia de Fibonacci, y se implementa de tres maneras:

• regularFib: usando la relación de recurrencia
  • $f_0 = 0, f_1 = 1, f_n = f_{n-1} + f_{n -2}$
• constexprFib: la misma fórmula pero haciendo la función constexpr
• binetsFib: usando la Fórmula de Binet¹
  • $f_n = \frac{ (1 + \sqrt{5} )^{n} - (1- \sqrt{5})^{n} } { 2^{n} * \sqrt{5} }$

El siguiente caso de prueba contiene las tres pruebas de referencia compiladas con GCC:

TEST_CASE("should benchmark different fib(25)", "[fibonacci]")
{
  BENCHMARK("regular   de n=25") { return regularFib(25); };
  BENCHMARK("constexpr de n=25") { return constexprFib(25); };
  BENCHMARK("Binet     de n=25") { return binetsFib(25); };
}

El resultado para 100 muestras:

Nombre	Iteraciones	Estimado	Media	Desviación (σ)
regular	1	53.1851 ms	525.406 us	24.0403 us
constexpr	1	50.9678 ms	504.298 us	14.0223 us
Binet’s	332	5.8432 ms	169.063 ns	13.1453 ns

Se observa que usando la Fórmula de Binet se logra un tiempo de ejecución medio de ~169 nanosegundos, muy superior a la fórmula regular (~525 microsegundos).

La diferencia puede ser considerablemente menor para números inferiores en la secuencia. También puede variar usando otro compilador, como clang.

Quick bench

Es un sitio web que usa google benchmark para escribir pruebas de referencia. En la imagen se muestran los resultados de ejecutar las pruebas para el elemento 5 de la secuencia, usando gcc.

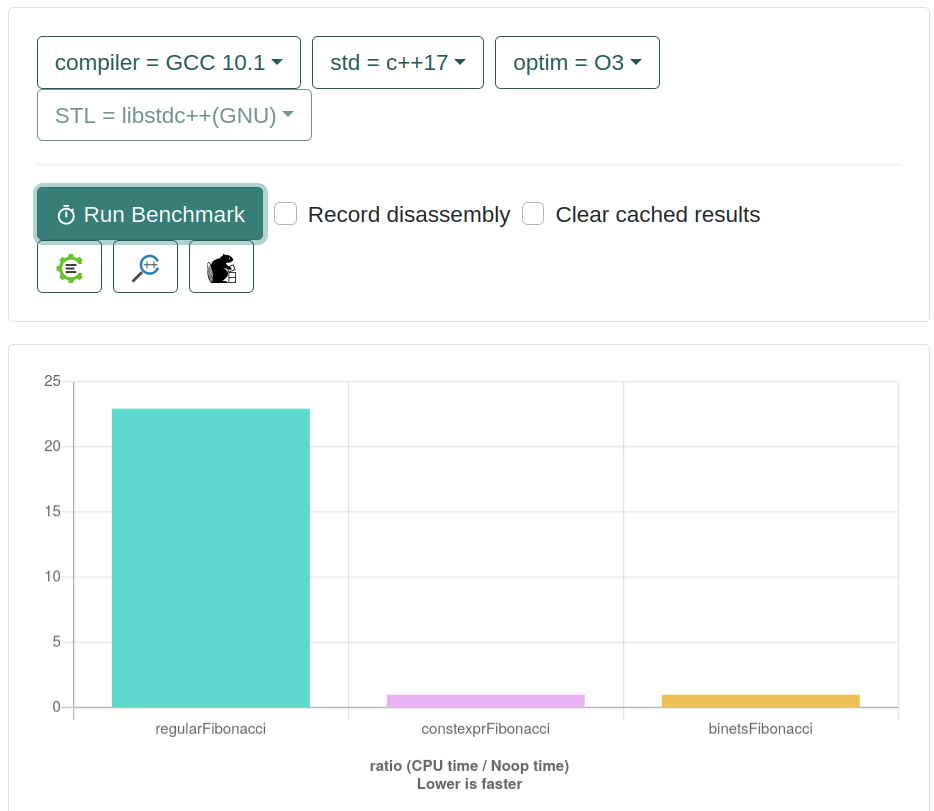
Se puede observar que usando la Fórmula de Binet se obtiene un resultado cercano a 20 veces más rápido que usando la fórmula de relación de recurrencia.

Fuentes

• De bfilipek: micro-benchmarking libraries
• De Vorbrodt: Micro-benchmark
• Acerca de nonius
• Quick benck

---

1. Ver Binet’s formula ↩